全部展开
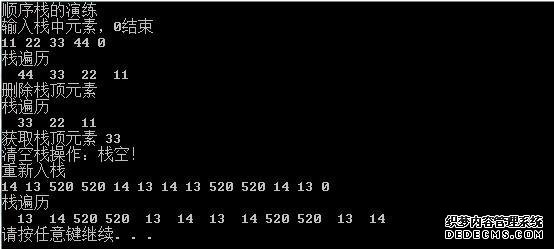
当堆叠顺序为a，b，c，d
问题1：因此，堆栈的顺序可能是a，b，c，d。然后，您可以删除堆栈，而无需等待其他项出现在数据中问题2：堆栈顺序中有多种类型的响应。
N个数据输入堆栈（C（2n，n）/（n +1）[C（n，m）代表所选的nm组合数）。
）种子堆放方案。
具体分析如下。每按一次，每个数字必须显示一次。
将插入状态设置为“ 1”，将弹出窗口状态设置为“ 0”。
n个数字的每个状态对应于一个由n 1和n 0组成的2位二进制数。
因为等待堆栈的操作数是按1顺序排列的？因为堆栈操作数b的n大于或等于堆栈a的操作数a（a≤b），所以从左到右依次扫描n1和n个二进制数，其中输出序列的总数为0。，累积数字1大于累积数字0。
在2n位二进制数中完成n 1个的方案的数量为c（2n，n），其余未填充1的n位自动填充为0。
获得了不满足要求的方案数量（从左到右扫描，累计数量0大于1）。
不满足要求的数值的特征是，如果从左向右扫描，则必须首先在特定的奇数位2m +1位2（nm）在位置1有nm 1和nm-10。
如果交换了最后2（nm）-1位0和1，它们分别变为nm 0和nm-1 1，则结果为1，由n + 1 0和n-1 1组成。这些位或不必要的数字对应于一个由n + 1 0s和n-1 1s组成的数组。
相反，由n + 1 0和n-1 1组成的2n位二进制数必须具有0累积数，因为0的数目是2，而2n是偶数。1或更多累积
同样在最后一部分中，交换0和1由n 0和n 1 2个数字组成。即，n +1 0和n-1 1 2n位必须对应于不满足要求的位。
因此，不必要位数2n对应于n + 1 0，n-1 1s的数组。
显然，不满足要求的方案数为c（2n，n + 1）。
这给出了输出序列的总数= c（2n，n）-c（2n，n + 1）= 1 /（n + 1）* c（2n，n）