热门文章
随机文章
向量组的范围是多少?
向量组的范围是多少?
全部展开
简而言之,如果该组中有5个向量,则假设抛出2个垃圾并剩下3个,则这是在去除这组向量中的垃圾向量之后将保留的高质量向量的数量。
因此,该组的向量范围是3。
那么什么是垃圾向量?
可以由其他人线性表达的向量。
例如,向量α1可以与α2和α3线性表达。换句话说,您可以用另一个作业替换该作业。
所以α1是一个垃圾向量!
等级是线性代数中最重要的概念,也是大多数应试者必须主导的概念。
线性代数有两个主要的范围类别。矩阵范围和向量组范围。这两个概念与区别有关。
首先让我们看一下每个概念。
矩阵范围:除矩阵A以外的零阶子窗体的顺序称为矩阵A范围,并表示为r(A)。其中,r(A)是不超过矩阵中最小行数的列数。
矩阵范围可以计算为向量组范围。向量组范围也可以计算为矩阵范围。
在计算矩阵范围时,理论上需要计算和确定一个非零子形式,但是计算量很大,有时很复杂,因此通过行转换将矩阵转换为交错矩阵。您基本上可以在末尾使用非零行数,这是一个矩阵范围。
扩展数据:根据向量组的范围,我们可以从线性独立定理1α1,α2,...,αs中的R{α1,α2,...,αs}= s得出一些有用的向量组我可以
如果向量组α1,α2,...,Α可以由向量组β1,β2,线性表达。…,Βt}。
三组等效向量的范围相等。
4如果向量α1,α2,...,αs的组是线性独立的,并且可以由向量β1,β2,...,βt的组线性表示,则s小于或等于t。
五组向量α1,α2,…,αs可以由向量β1,β2,…,βt和st的组线性表示,而α1,α2,…,αs线性相关。
六个任意的n +1个n维向量线性相关。
具有矢量组范围的矩阵范围的概念可以导致矩阵范围的概念。
m×n数组可以看作是由m行向量组成的一组行向量,也可以看作是由n列向量组成的一组列向量。
您可以轻松地显示出行向量组的等级变为行范围,列向量组的范围变为等级范围,并且行的等级等于等级的等级。那可能是矩阵的等级。
矩阵范围在线性代数中有很大的用途,可用于计算逆矩阵并确定线性方程的解。
请参阅:百科全书百度-向量组范围
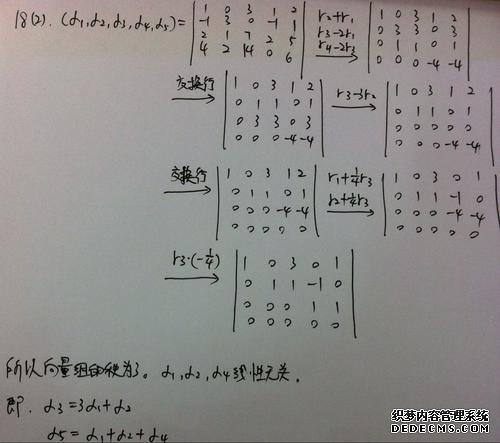
简而言之,如果该组中有5个向量,则假设抛出2个垃圾并剩下3个,则这是在去除这组向量中的垃圾向量之后将保留的高质量向量的数量。
因此,该组的向量范围是3。
那么什么是垃圾向量?
可以由其他人线性表达的向量。
例如,向量α1可以与α2和α3线性表达。换句话说,您可以用另一个作业替换该作业。
所以α1是一个垃圾向量!
等级是线性代数中最重要的概念,也是大多数应试者必须主导的概念。
线性代数有两个主要的范围类别。矩阵范围和向量组范围。这两个概念与区别有关。
首先让我们看一下每个概念。
矩阵范围:除矩阵A以外的零阶子窗体的顺序称为矩阵A范围,并表示为r(A)。其中,r(A)是不超过矩阵中最小行数的列数。
矩阵范围可以计算为向量组范围。向量组范围也可以计算为矩阵范围。
在计算矩阵范围时,理论上需要计算和确定一个非零子形式,但是计算量很大,有时很复杂,因此通过行转换将矩阵转换为交错矩阵。您基本上可以在末尾使用非零行数,这是一个矩阵范围。
扩展数据:根据向量组的范围,我们可以从线性独立定理1α1,α2,...,αs中的R{α1,α2,...,αs}= s得出一些有用的向量组我可以
如果向量组α1,α2,...,Α可以由向量组β1,β2,线性表达。…,Βt}。
三组等效向量的范围相等。
4如果向量α1,α2,...,αs的组是线性独立的,并且可以由向量β1,β2,...,βt的组线性表示,则s小于或等于t。
五组向量α1,α2,…,αs可以由向量β1,β2,…,βt和st的组线性表示,而α1,α2,…,αs线性相关。
六个任意的n +1个n维向量线性相关。
具有矢量组范围的矩阵范围的概念可以导致矩阵范围的概念。
m×n数组可以看作是由m行向量组成的一组行向量,也可以看作是由n列向量组成的一组列向量。
您可以轻松地显示出行向量组的等级变为行范围,列向量组的范围变为等级范围,并且行的等级等于等级的等级。那可能是矩阵的等级。
矩阵范围在线性代数中有很大的用途,可用于计算逆矩阵并确定线性方程的解。
请参阅:百科全书百度-向量组范围

